저번 글에서 알아봤던 KMP 알고리즘을 활용하여 풀 수 있는 문제들에 대해 알아본다.
1. 문자열 제곱(https://www.acmicpc.net/problem/4354)
문자열 a의 n 제곱을 문자열 a를 n번 이어붙이는 연산으로 정의하고(ex) 'abc'^3 == 'abcabcabc') 문자열 s가 주어졌을 때, s 를 a^n 을 만족하는 가장 큰 n을 구하는 문제.
KMP 알고리즘 전체가 아니라 KMP 알고리즘에서 사용했던 실패함수, 즉 LPS를 구하는 알고리즘을 활용하여 풀 수 있는 문제이다. 문제로 주어진 각 케이스들은 문자열 s 의 lps값에 따라 다음의 세 가지 경우로 나눌 수 있다.
# case 1) len(lps)*2 < len(s)

len(lps) * 2(양 끝의 lps 길이를 더한 값)가 문자열의 길이보다 짧을 경우, 해당 문자열은 어떤 문자열의 반복으로 나타낼 수 없다. lps에 속하지 않은 문자열을 표현할 방법이 없기 때문이다. 이 경우 s = s ^ 1 로 밖에 나타낼 수 없기 때문에 답은 1이 된다.
# case 2) len(lps)*2 == len(s)

len(lps) * 2 가 문자열의 길이와 같을 경우, 해당 문자열은 lps ^ 2 로만 나타낼 수 있다. n이 더 커지려면 lps 자체도 문자열의 반복으로 이루어져야 하는데, 그렇게 될 경우 당연히 lps는 더 길어지기 때문에 그런 경우는 있을 수 없다. 답은 2가 된다.
# case 3) len(lps)*2 > len(s)

이 경우는 또다시 두 가지 경우로 나뉘어진다. 두 LPS가 겹친 부분의 문자열을 v, lps에서 공통부분을 뺀 문자열을 u 라고 하자. 이때 len(v)가 len(u)의 배수가 된다면 s = u ^ ((v // u) + 2) 로 나타낼 수 있게된다. 이 경우에 답은 v // u + 2 가 된다.

만약 len(v) 가 len(u) 의 배수가 아니라면 문자열 s는 반복되는 문자열로 나타낼 수 없다. s = s ^ 1 로 밖에 나타낼 수 없기 때문에 이 경우에 답은 1이 된다.
이 사실을 토대로 문제를 해결한 코드는 다음과 같다.
import sys
input = sys.stdin.read
def sol4354():
# 각 케이스의 정답을 저장할 리스트
answer = []
# 케이스의 문자열 s
for s in input().splitlines():
# s가 '.'이라면 종료
if s == '.':
break
# lps 테이블 전처리
m = len(s)
dp = [0]*m
i = 0
for j in range(1, m):
while i > 0 and s[i] != s[j]:
i = dp[i-1]
if s[i] == s[j]:
i += 1
dp[j] = i
# 공통부분 v
v = dp[-1] * 2 - m
# 공통부분의 길이가 0보다 작은 경우
# lps * 2 < m 이기 때문에 답은 1
if v < 0:
answer.append(1)
# 공통부분의 길이가 0인 경우
# lps * 2 == m 이기 때문에 답은 2
elif v == 0:
answer.append(2)
# 공통부분의 길이가 1 이상인 경우
else:
# lps에서 공통부분을 뺀 길이
u = dp[-1] - v
# v가 u의 배수가 아니라면
# 반복되는 문자열로 나타낼 수 없기 때문에 답은 1
if v % u:
answer.append(1)
# v가 u의 배수라면
# 양 끝의 u와 중간의 v//u 개의 u를 이어붙인 형태이기 때문에
# u ^ (v//u + 2) 로 나타낼 수 있음.
# 답은 v//u + 2
else:
answer.append(v//u+2)
# 정답 리스트를 출력형식에 맞춰 반환
return '\n'.join(map(str, answer))
2. 광고(https://www.acmicpc.net/problem/1305)
길이 L의 전광판에 길이 N의 광고문구를 무한히 이어붙인 문자열이 표시될 때, 광고문구가 될수있는 가장 짧은 문자열의 길이를 구하는 문제. 예를들어 길이가 6인 광고판에 aabaaa가 표시된 경우 원래 광고로 추정 가능한 가장 짧은 것은 'aaba', 'aaab', 'baaa', 'abaa' 등이다.
이 문제 또한 KMP 알고리즘의 실패함수를 활용하여 해결할 수 있다. 전광판에 표시된 문자열이 광고를 무한히 이어붙인 형태라면 문자열 내에는 광고의 시작부분이 반복되는 구간이 존재한다. 이를 문자열의 lps라고 생각하면 나머지는 간단하다. 예시로 든 'aabaaa' 의 경우, lps 는 'aa' 가 된다. 그러면 'aabaaa' 에서 suffix에 해당하는 'aa' 는 광고가 이어붙여진 부분이라고 생각할 수 있다. 이렇게 생각할 경우 이 광고의 원래 형태는 'aaba' + 'aaba' + 'aaba' ... 가 된다. 그리고 이것이 가능한 광고의 가장 짧은 형태이다. 즉, 전광판의 길이 L과 문자열 s가 주어졌을 때, 가능한 광고 길이의 최솟값은 L - len(lps) 가 된다. 이 사실을 토대로 문제를 해결한 코드는 다음과 같다.
import sys
input = sys.stdin.readline
def sol1305():
# 전광판의 크기
L = int(input())
# 전광판에 표시된 문자열
adv = input().rstrip()
# LPS 테이블 전처리
lps = [0] * L
i = 0
for j in range(1, L):
while i > 0 and adv[i] != adv[j]:
i = lps[i-1]
if adv[i] == adv[j]:
i += 1
lps[j] = i
# L - len(lps) 반환
return L-lps[-1]
3. 시계 사진들(https://www.acmicpc.net/problem/10266)
동일한 길이의 바늘 n 개를 가진 두 시계의 각 바늘이 9시방향과 이루는 각도가 순서없이 주어졌을 때, 두 시계를 회전시켜 같은 시간을 가리키도록 할 수 있는지 구하는 문제. 각도의 단위는 1/1000도(degree)이다.
문제해결의 가장 중요한 아이디어는 바늘을 건드리지않고 두 시계를 회전시켜 같은 시간을 가리키도록 할 수 있으려면 두 시계의 인접한 바늘들이 서로 같은 각도만큼 떨어져있어야 한다는 것이다. 문제를 해결한 절차는 다음과 같다.
① 두 시계의 시계바늘의 각도들을 오름차순으로 정렬한다.
② 각 시계의 인접한 바늘끼리의 각도의 차를 구한다.(A, B) 이 때, 마지막 각도와 첫 번째 각도의 차도 구해야함에
유의해야 하며, 마지막 바늘에서 시작하여 첫 바늘로 가는 각도이기 때문에 An = D1 - (Dn - 360000) 와 같이
계산해야한다.
③ 시계를 회전시키는 것으로 같은 시각을 가리키게 할 수 있으려면 인접한 바늘의 각도차 리스트 A, B중 한쪽을
회전시켜가며 비교해야한다.
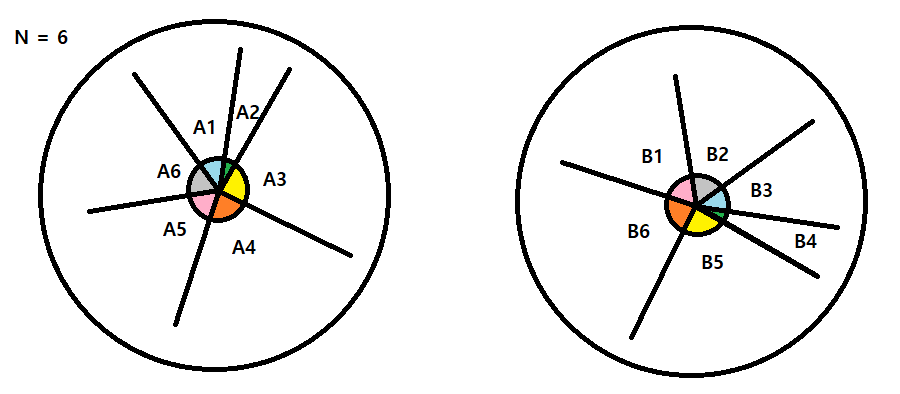
위 그림의 두 시계를 회전하여 같은 시각을 가리키도록 만들 수 있는지 확인하기 위해 인접한 바늘들의 각도차 리스트
A = [A1, A2, A3, A4, A5, A6] 와 B = [B1, B2, B3, B4, B5, B6] 를 비교해야한다. 그런데 A나 B 한쪽을 회전시켜가며 비교하는 것은 O(N^2) 의 시간복잡도를 가지기 때문에 N의 최대 크기가 20만인 이 문제를 1초안에 해결할 수 없다. 하지만 KMP 알고리즘을 활용하면 이 문제를 간단히 해결할 수 있다.
④ 리스트 A를 회전시킨 결과 B와 일치하는 경우가 존재한다면 A를 두번 이어붙인 리스트에 B와 일치하는 구간이
존재한다고도 생각할 수 있다. 즉, 리스트 A를 두번 이어붙인 리스트에서 리스트 B가 등장하는지 KMP 알고리즘으로
검사한다면 O(N)의 시간복잡도로 이 작업을 해결할 수 있다.
위 사실을 토대로 문제를 해결한 코드는 다음과 같다.
import sys
input = sys.stdin.readline
def sol10266():
# 시계의 바늘 갯수
n = int(input())
# 두 시계의 바늘의 각도를 오름차순 정렬
x = sorted(map(int, input().split()))
y = sorted(map(int, input().split()))
# 인접한 바늘끼리의 각도차 리스트를 구함
a = ([x[(i + 1)] - x[i] for i in range(n - 1)] + [x[0] - (x[-1] - 360000)]) * 2
b = [y[(i + 1)] - y[i] for i in range(n - 1)] + [y[0] - (y[-1] - 360000)]
n, m = 2 * n, n
# LPS 테이블 전처리
lps = [0] * (m + 1)
i = 0
for j in range(1, m):
while i > 0 and b[i] != b[j]:
i = lps[i - 1]
if b[i] == b[j]:
i += 1
lps[j] = i
# KMP 알고리즘으로 문자열 탐색 시작
i, j = 0, 0
while i < n:
if a[i] == b[j]:
i += 1
j += 1
# 탐색에 성공했다면 같은 시각을 나타내도록 할 수 있음
# 'possibe' 반환
if j == m:
return 'possible'
else:
if j == 0:
i += 1
j = lps[j - 1]
# 모든 작업을 마칠동안 탐색에 성공하지 못했다면
# 같은시각을 나타내도록 할 수 없음
# 'impossible' 반환
return 'impossible'
KMP 알고리즘을 통한 문자열 검색 자체도 활용도가 높지만 실패함수도 활용도가 상당히 높다는걸 알 수 있었다.
필요하다면 언제든지 구현할 수 있도록 기억해두는 것이 좋겠다.
'코딩테스트 > 알고리즘' 카테고리의 다른 글
| #32 문자열 탐색 - 트라이(Trie) 2 (0) | 2021.09.09 |
|---|---|
| #32 문자열 탐색 - 트라이(Trie) 1 (0) | 2021.09.08 |
| #30 문자열 탐색 - KMP 알고리즘(1) (0) | 2021.09.06 |
| #29 동적 계획법 4 - 경우의 수 (0) | 2021.09.04 |
| #28 동적 계획법(Dynamic Programming) 3 - 비트마스크(Bit Mask) (0) | 2021.09.03 |