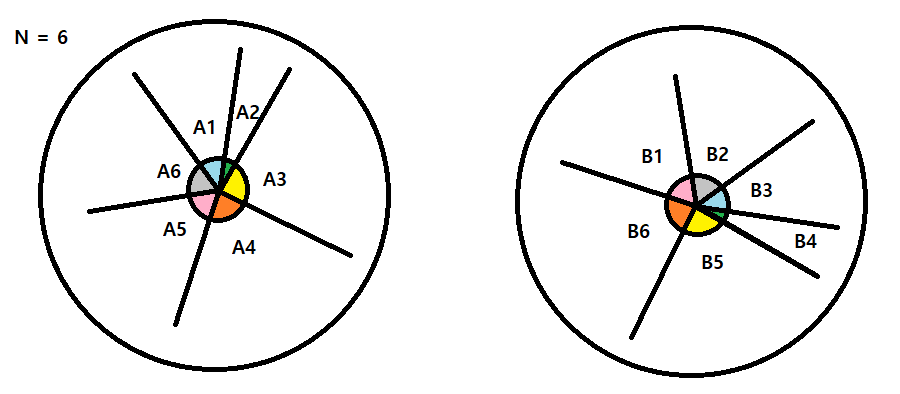
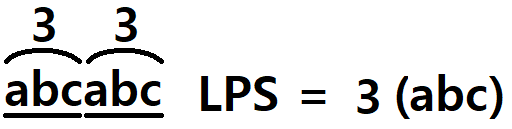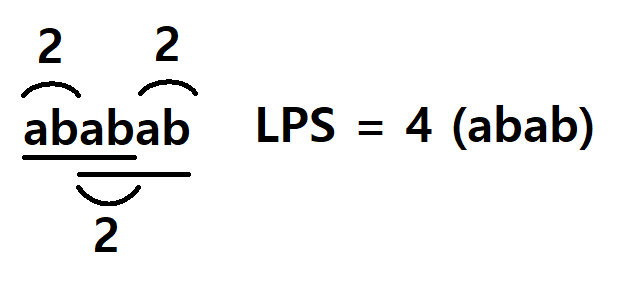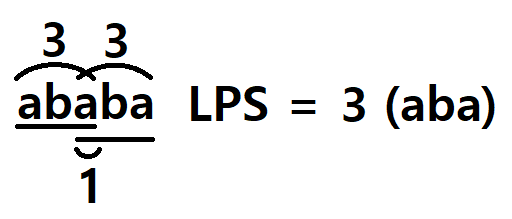트리에서 두 노드의 가장 가까운 공통 조상을 보다 효율적으로 구하기 위한 LCA 알고리즘에 대해 관련 문제를 해결하며 알아본다.
1. 가장 가까운 공통 조상(https://www.acmicpc.net/problem/3584)
가장 기본적인 LCA 문제이다. 노드의 수가 최대 10,000이며 쿼리의 수도 하나 뿐이기 때문에 효율적인 알고리즘을 생각할 필요 없이 간선 정보를 토대로 각 노드의 부모노드를 저장하고 쿼리로 주어진 두 노드로부터 부모노드를 탐색해나가며 각 노드의 모든 조상노드 리스트를 구하고, 두 리스트를 뒤에서부터 비교해나갔을 때 마지막으로 같았던 두 리스트의 값이 가장 가까운 공통 조상 노드가 된다. 이를 구현한 코드는 다음과 같다.
import sys
input = sys.stdin.readline
# 3584 가장 가까운 공통 조상
# 노드의 수가 적고 쿼리도 케이스당 하나 뿐이기 때문에
# 단순한 방식으로도 해결 가능
def sol3584():
# 케이스별 정답 리스트
answer = []
for t in range(int(input())):
# 노드의 수
n = int(input())
# 각 노드의 부모노드
parent = [0] * (n + 1)
# 부모노드와 자식노드를 입력받아 부모노드를 채운다
for _ in range(n - 1):
a, b = map(int, input().split())
parent[b] = a
# 가장 가까운 공통조상을 구할 두 노드
u, v = map(int, input().split())
# 두 노드의 조상 노드 리스트를 구한다.
up, vp = [], []
while u:
up.append(u)
u = parent[u]
while v:
vp.append(v)
v = parent[v]
# 두 노드의 조상 노드 리스트를 뒤집는다.
up, vp = up[::-1], vp[::-1]
# 루트 노드부터 시작하여 두 노드의 조상 노드가 서로 달라질 때 까지 탐색
# 두 노드의 조상 노드가 마지막으로 같았을 때의 조상 노드가 가장 가까운 공통 조상 노드가 된다.
res = 0
for i in range(min(len(up), len(vp))):
if up[i] == vp[i]:
res = up[i]
else:
break
# 정답 리스트에 결과 삽입
answer.append(res)
# 출력 형식에 맞춰 정답 리스트 반환
return '\n'.join(map(str, answer))
하지만 위의 방법은 당연하게도 노드의 수와 쿼리의 수가 많아지면 쿼리마다 사용할 수 없다.
이번엔 다른 방식으로 문제를 해결해보자. 절차는 다음과 같다.
① 먼저 트리를 탐색하여 모든 노드의 깊이와 부모노드를 구한다.
② 주어진 두 노드의 깊이가 다르다면 보다 깊이 있는 노드가 다른 노드와 같은 높이가 될 때 까지 거슬러 올라온다.
③ 두 노드가 서로 같아질 때 까지 두 노드 모두 부모노드를 타고 거슬러 올라온다.
④ 두 노드가 서로 같아졌을 때, 그 노드가 가장 가까운 조상 노드가 된다.
이를 구현한 코드는 다음과 같다.
import sys
input = sys.stdin.readline
def sol3584():
# 정답 리스트
answer = []
# 테스트케이스
for t in range(int(input())):
# 노드의 수
n = int(input())
# 그래프 생성, 부모 노드 구하기
g = [[] for _ in range(n + 1)]
parent = [0] * (n + 1)
for _ in range(n-1):
a, b = map(int, input().split())
g[a].append(b)
parent[b] = a
# 루트 노드로부터 bfs탐색으로 각 노드의 깊이를 구한다
depth = [0] * (n + 1)
root = [i for i in range(1, n+1) if not parent[i]][0]
q = [root]
while q:
nq = []
for cur in q:
for c in g[cur]:
depth[c] = depth[cur] + 1
nq.append(c)
q = nq
# 주어진 두 노드 u, v
u, v = map(int, input().split())
# 노드 u의 깊이가 노드 v의 깊이보다 크도록 한다.
if depth[u] < depth[v]:
u, v = v, u
# 두 노드의 깊이차가 0이 될 때 까지 깊은 쪽 노드인 u를 끌어올린다
while depth[u] - depth[v]:
u = parent[u]
# 두 노드가 서로 같아질 때 까지 두 노드를 끌어올린다
while u != v:
u, v = parent[u], parent[v]
# u와 v가 서로 같아지면 u == v == 가장 가까운 공통 조상 노드 가 된다.
answer.append(u)
# 출력 형식에 맞춰 정답 리스트 반환
return '\n'.join(map(str, answer))이 방식 자체로는 보다 많은 노드와 쿼리 수가 주어지는 문제를 해결하기에 딱히 이전의 알고리즘보다 효율적이지 않다. 하지만 이 방식에 sparse table을 적용하면 얘기가 달라진다. 다음 문제에서 이 sparse table에 대해 다룬다.
2. 합성함수와 쿼리(https://www.acmicpc.net/problem/17435)
함수 f(x)의 값들이 주어졌을때, fn(x) 가 f(f(f(...f(x)...))) 와 같이 함수 f를 n중첩한 결과라고 한다. 이 때, 주어진 m개의
n, x 쌍에 대해 fn(x) 를 각각 구하는 문제이다. LCA 문제는 아니지만 LCA 알고리즘의 핵심인 sparse table을 응용해서
풀 수 있는 문제이다. 절차는 다음과 같다.
① 먼저 함수 f의 값을 저장할 2차원 배열을 생성한다. 이 때, f[x][k] 는 함수 f의 k중첩에 x를 넣은 결과이다. 예를들어,
f[3][4] = f(f(f(f(3)))) 이 된다.
② f[x][0] 의 값을 입력받은 f(x)의 값으로 초기화한다.
③ f[i][j] 은 f[i][j-1] 을 2^(j-1) 중첩한 값이 되기 때문에, 점화식 f[i][j] = f[f[i][j-1]][j-1] 이 성립한다. 이 점화식에 따라
나머지 f[x][1~k] 를 채운다. 여기서 k는 함수 중첩수 최댓값인 n에 로그를 취한 뒤 올림한 값이 된다.
=> math.ceil(math.log2(n))
④ 이제 쿼리로 n, x가 주어지면 ③ 에서 구한 sparse table을 이용하여 빠르게 목표한 값으로 접근한다.
n이 0보다 큰 동안, x = f[x][int(log2(n))]; n -= (1 << int(log2(n))) 을 수행하면 가능하다. n 중첩을
1씩 좁혀나가는 것이 아니라 2의 승수단위로 좁혀나가는 것으로 탐색시간을 극적으로 줄이는 방식이다.
⑤ ④의 작업이 모두 끝났을 때, x의 값이 해당 쿼리에 대한 정답이 된다.
import sys
from math import log2, ceil
input = sys.stdin.readline
def sol17435():
# 주어진 함수값의 수
m = int(input())
# 500000 <= 2^k
k = ceil(log2(500000))
# sparse table : f[x][k] = fk(x)
f = [[-1] * k for _ in range(m + 1)]
fn = list(map(int, input().split()))
for i in range(m):
f[i + 1][0] = fn[i]
# 점화식 f[i][j] = f[f[i][j-1]][j-1] 에 따라 sparse table 나머지 채우기
for j in range(1, k):
for i in range(1, m + 1):
f[i][j] = f[f[i][j - 1]][j - 1]
# 쿼리의 수
q = int(input())
# 각 쿼리의 정답 구하기
answer = []
for _ in range(q):
# 함수 중첩수 n, 인자값 x
n, x = map(int, input().split())
# 중첩수가 0이 되면 종료
while n:
# f[x][d] == f2^d(x)
d = int(log2(n))
x = f[x][d]
# 2^d 중첩만큼 처리했기 때문에 남은 중첩수에서 감산
n -= (1 << d)
# 정답리스트에 쿼리의 정답 저장
answer.append(x)
# 출력 형식에 맞춰 정답 리스트 반환
return '\n'.join(map(str, answer))sparse table은 말그대로 어떤 규칙에 따른 값을 지수단위로 듬성듬성하게 구해두고 원하는 값까지 로그시간으로
빠르게 접근하기 위한 자료구조이다. 이 문제의 경우 sparse table 은 구성하는데에 O(MlogN)의 시간복잡도를,
쿼리 하나를 처리하는데 O(logN) 의 시간복잡도를 보인다.(경우에 따라서는 O(1) 수준의 성능을 보일때도 있다고 한다.)
sparse table은 정적인 데이터에서의 쿼리만을 처리할 수 있기 때문에 동적 데이터(데이터가 삽입, 삭제, 변경되는 경우)
에는 대응이 불가능하다. 만약 정적인 데이터에 대해 대량의 쿼리를 처리해야하는 경우라면 sparse table을 사용하는
것을 고려해볼만 할 것 같다.
3. LCA 2 (https://www.acmicpc.net/problem/11438)
이제 1번 문제에서 두 번째로 사용했던 알고리즘에 sparse table을 적용할 차례다. 노드의 수가 최대 100,000개로
늘어나고 쿼리의 수도 최대 100,000개이기 때문에 O(NM)의 시간복잡도를 보이는 기존의 방식으로는 해결할 수 없다.
두 노드의 깊이를 동일하게 맞추는 작업과 동일한 깊이에 있는 두 노드의 가장 가까운 조상 노드를 찾아가는 작업을
sparse table을 사용하여 O(logN) 수준으로 최적화한다. 이를 구현한 코드는 다음과 같다.
import sys
import math
input = sys.stdin.readline
# sparse table(희소 테이블)을 활용하여 문제를 더 효율적으로 해결할 수 있다. 절차는 다음과 같다.
# 1. 각 노드의 깊이를 나타낼 depth 리스트와 부모노드를 나타낼 parent 리스트를 생성한다
# 이 때, parent 리스트는 2차원 리스트이며 parent[i][k] 는 노드 i의 2^k 번 거슬러올라간 조상노드를 의미한다.
#
# 2. dfs 혹은 bfs 로 트리를 순회하며 각 노드의 1번 거슬러올라간 조상노드(parent[i][0])와 깊이를 구한다.
# 이 때, 점화식 parent[i][j] = parent[parent[i][j-1]][j-1] 를 사용해서 O(NK) 의 시간 복잡도로 작업을 수행한다.
# K는 log(2, N) 을 올림한 값과 같다.
#
# 3. 각 질의(LCA 를 구할 두 노드 u, v) 에 대해 두 노드의 깊이가 같아질 때 까지
# 보다 깊이가 큰 노드를 끌어올린다.
#
# 4. 두 노드가 서로 같다면 그대로 어느 한쪽 노드를 출력
#
# 5. 그렇지 않다면 두 노드의 가장 먼 공통 조상으로부터 처음으로 두 노드의 조상 노드가 달라질 때 까지 탐색
# 탐색 종료 후 노드 u 또는 v의 부모노드를 출력
def sol11438():
# 각 노드의 깊이와 첫 번째 부모를 구하기 위한 탐색 함수
def bfs(root):
q = [root]
while q:
nq = []
for cur in q:
for c in g[cur]:
if depth[c] < 0:
depth[c] = depth[cur] + 1
parent[c][0] = cur
nq.append(c)
q = nq
# 노드의 수
n = int(input())
# sparse table 의 크기
k = math.ceil(math.log2(n))
# 그래프 생성
g = [[] for _ in range(n + 1)]
for _ in range(n - 1):
a, b = map(int, input().split())
g[a].append(b)
g[b].append(a)
# 각 노드의 깊이 리스트
depth = [-1] * (n + 1)
# 각 노드의 조상 노드 리스트 (sparse table)
parent = [[-1] * k for _ in range(n + 1)]
# 루트 노드인 1의 깊이를 0으로 하고 탐색 시작
depth[1] = 0
bfs(1)
# sparse table 채우기
for j in range(1, k):
for i in range(1, n + 1):
parent[i][j] = parent[parent[i][j - 1]][j - 1]
# 각 질의에 대해 정답 구하기
answer = []
for _ in range(int(input())):
u, v = map(int, input().split())
# 노드 u가 노드 v 보다 깊이가 크도록 한다
if depth[u] < depth[v]:
u, v = v, u
# 두 노드의 깊이가 같아질 때 까지 노드 u를 끌어올린다
while depth[u] - depth[v]:
u = parent[u][int(math.log2(depth[u] - depth[v]))]
# 두 노드가 같지 않다면
if u != v:
# 가장 먼 공통 조상 노드로부터 처음으로 두 노드의 조상 노드가 달라질 때 까지 탐색
for j in range(math.ceil(math.log2(depth[u])), -1, -1):
if parent[u][j] != parent[v][j]:
u = parent[u][j]
v = parent[v][j]
# 현재 u와 v는 공통 조상노드의 자식 노드인 상태이므로 둘 중 하나는 부모노드를 방문
u = parent[u][0]
# 노드 u 혹은 v를 반환
answer.append(u)
# 출력 형식에 맞춰 정답리스트 반환
return '\n'.join(map(str, answer))
'코딩테스트 > 알고리즘' 카테고리의 다른 글
| #36 위상 정렬(Topological Sorting) (0) | 2021.09.15 |
|---|---|
| #35 위상 정렬(Topological Sorting) (0) | 2021.09.14 |
| #34 누적 합(Prefix Sum) - 2차원 (0) | 2021.09.13 |
| #33 누적 합(Prefix Sum) - 1차원 (0) | 2021.09.11 |
| #32 문자열 탐색 - 트라이(Trie) 2 (0) | 2021.09.09 |