이전 글에서 다루었던 트라이 자료구조를 활용하여 해결할 수 있는 문제를 살펴본다.
1. 개미굴(https://www.acmicpc.net/problem/14725)
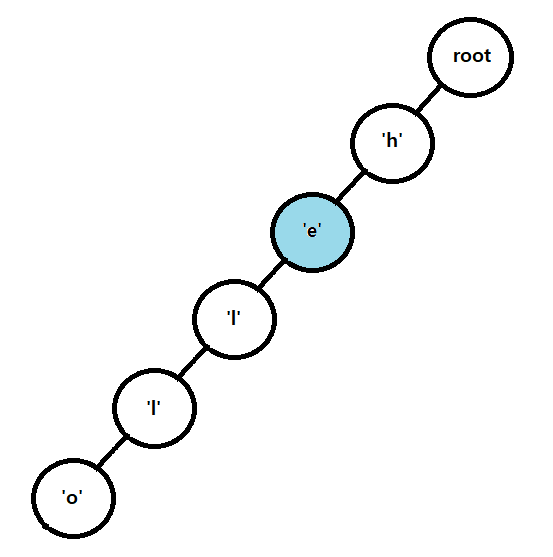
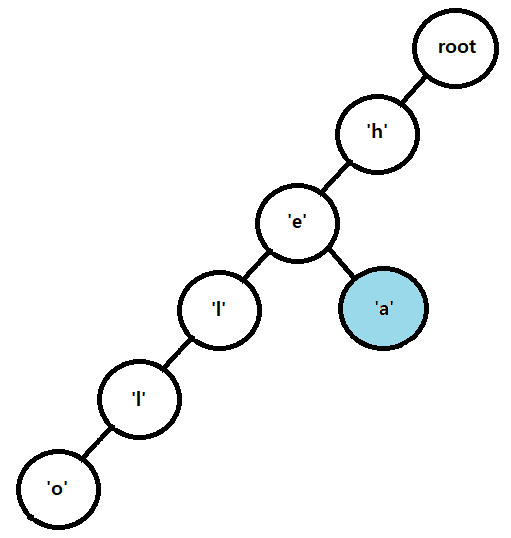
탐사용 개미로봇은 트리 형태를 이루는 개미굴을 입구(루트)부분에서 시작하여 아래로 내려가며 탐색을 진행하고 더이상 내려갈 수 없어지면 지금까지 거쳐온 방의 정보를 전송하고 작동을 중지한다. 개미로봇들이 보낸 정보를 토대로 개미굴의 형태를 그려내는 문제.
단순히 개미로봇이 보낸 정보들을 트라이에 삽입한 후 트라이의를 출력형식에 맞춰 문자열화하는 것으로 간단하게 해결 가능한 문제이다. 문제를 해결한 코드는 다음과 같다.
import sys
input = sys.stdin.readline
# 트라이의 노드 클래스
# data(키 값), child(자식노드 목록), finished(데이터의 마지막 노드인지 여부)의 세 필드값을 가진다.
class Node:
# 생성자
def __init__(self, data=None, finished=False):
self.data = data
self.finished = finished
self.child = {}
# 노드를 문자열로 표현
def __str__(self, depth=0):
res = [str(self.data)]
for c in self.child.values():
res.append('--' * depth + c.__str__(depth + 1))
return '\n'.join(res)
# 트라이 클래스
class Trie:
# 생성시 빈 노드를 생성하여 루트노드로 설정
def __init__(self):
self.root = Node()
# 삽입 메소드
def add(self, e):
# 루트 노드에서 탐색 시작
cur = self.root
# 데이터의 각 요소를 키 값으로 하는 노드를 타고내려간다.
for i in e:
# 현재 노드의 자식노드 중에
# 다음 요소를 키 값으로 하는 노드가 존재하지 않는다면 노드를 생성
# 현재 노드의 자식노드 리스트에 삽입한다.
if i not in cur.child:
cur.child[i] = Node(i)
cur = cur.child[i]
# 현재 노드가 데이터의 마지막 요소를 키값으로 하는 노드임을 표시
cur.finished = True
# 탐색 메소드
def search(self, key):
# 루트 노드에서 탐색 시작
cur = self.root
# 데이터의 각 요소를 키 값으로 하는 노드를 타고내려간다.
for c in key:
# 현재 노드의 자식노드 중에
# 다음 요소를 키 값으로 하는 노드가 존재하지 않는다면 노드를 생성
# 찾으려는 데이터가 존재하지 않음을 결과로 반환한다.
if c in cur.child:
cur = cur.child[c]
else:
return None
# 탐색이 종료됐을 때, 마지막 노드가 데이터의 마지막 요소를 키 값으로 하는 노드로
# 표시되어있다면 탐색 성공. 그렇지 않다면 데이터가 존재하지 않음을 결과로 반환한다.
return cur.data if cur.finished else None
# 트라이를 문자열로 표현
def __str__(self):
return '\n'.join([c.__str__(1) for c in self.root.child.values()])
def sol14725():
# 로봇개미의 수
n = int(input())
# 트라이 인스턴스
t = Trie()
# 로봇개미가 가져온 정보를 트라이에 삽입
for e in sorted([input().split()[1:] for _ in range(n)]):
t.add(e)
# 트라이 인스턴스를 문자열화 하여 반환
return str(t)
2. 문자열 집합(https://www.acmicpc.net/problem/14425)
N개의 문자열로 이루어진 집합 S 와 M개의 문자열이 주어졌을 때, M개중 몇 개의 문자열이 S에 속해있는지 구하는 문제. 사실 Python의 경우 set 등을 활용하여 더 빠르고 쉽게 해결할 수 있지만 연습을 위해 트라이를 사용하여 풀어보았다. 코드는 다음과 같다.
import sys
input = sys.stdin.readline
# 트라이의 노드 클래스
# data(키 값), child(자식노드 목록), finished(데이터의 마지막 노드인지 여부)의 세 필드값을 가진다.
class Node:
def __init__(self, data=None, finished=False):
self.data = data
self.finished = finished
self.child = {}
# 트라이 클래스
class Trie:
# 생성시 빈 노드를 생성하여 루트노드로 설정
def __init__(self):
self.root = Node()
# 삽입 메소드
def add(self, e):
# 루트 노드에서 탐색 시작
cur = self.root
# 데이터의 각 요소를 키 값으로 하는 노드를 타고내려간다.
for i in e:
# 현재 노드의 자식노드 중에
# 다음 요소를 키 값으로 하는 노드가 존재하지 않는다면 노드를 생성
# 현재 노드의 자식노드 리스트에 삽입한다.
if i not in cur.child:
cur.child[i] = Node(i)
cur = cur.child[i]
# 현재 노드가 데이터의 마지막 요소를 키값으로 하는 노드임을 표시
cur.finished = True
# 탐색 메소드
def search(self, key):
# 루트 노드에서 탐색 시작
cur = self.root
# 데이터의 각 요소를 키 값으로 하는 노드를 타고내려간다.
for c in key:
# 현재 노드의 자식노드 중에
# 다음 요소를 키 값으로 하는 노드가 존재하지 않는다면 노드를 생성
# 찾으려는 데이터가 존재하지 않음을 결과로 반환한다.
if c in cur.child:
cur = cur.child[c]
else:
return None
# 탐색이 종료됐을 때, 마지막 노드가 데이터의 마지막 요소를 키 값으로 하는 노드로
# 표시되어있다면 탐색 성공. 그렇지 않다면 데이터가 존재하지 않음을 결과로 반환한다.
return cur.data if cur.finished else None
def sol14425():
# 집합에 속한 문자열의 갯수 N, 검사할 문자열의 갯수 M
n, m = map(int, input().split())
# 입력된 모든 문자열
strings = sys.stdin.read().split()
# N개의 문자열을 트라이에 삽입
t = Trie()
for i in range(n):
t.add(strings[i])
# M개의 문자열을 모두 탐색하여 몇 개의 문자열이 트라이에 존재하는지 센다
cnt = 0
for i in range(n, n + m):
cnt += (1 if t.search(strings[i]) else 0)
# 결과반환
return cnt단순히 N개의 문자열을 모두 트라이에 넣고 M개의 문자열에 대해 탐색을 진행하는 것으로 해결한 풀이이다. 시간복잡도는 1<=L(문자열 최대길이)<=500, 1<=N<=10,000, 1<=M<=10,000 일 때 O(L(N+M)) 의 시간복잡도를 보이기에 PyPy3으로만 AC를 받을 수 있었다. Python3으로는 추후에 좀더 최적화를 거쳐 다시 제출해보기로 한다.
3. 휴대폰 자판(https://www.acmicpc.net/problem/5670)
자동완성 기능을 가진 휴대폰 자판으로 단어들을 타이핑할 때 필요한 타이핑 횟수의 평균값을 구하는 문제. 사전에 속해있는 단어의 갯수 N이 최대 10만이며 각 케이스에 주어지는 단어 길이의 총합도 100만으로 상당히 많은 양의 데이터를 처리해야하기 때문에 모든 단어마다 실제로 시뮬레이션을 돌려보는것은 시간초과가 발생할 것이다.
각 단어가 삽입될 때, 거쳐간 노드의 카운트를 1씩 증가시키는 것으로 해당 노드가 몇개의 단어에 포함되어있는지 파악하고, dfs로 모든노드를 탐색하며 눌리지 않을 버튼을 키값으로 하는 노드를 제외한 모든 노드의 카운트값을 더하는 것으로 눌러야할 버튼 수 의 총합을 구할 수 있다. 문제를 해결한 코드는 다음과 같다.
import sys
input = sys.stdin.readline
# 트라이의 노드 클래스
# data(키 값), child(자식노드 목록), finished(데이터의 마지막 노드인지 여부), cnt(거쳐간 단어의 수)의 네 개의 필드값을 가진다.
class Node:
def __init__(self, data=None, finished=False):
self.data = data
self.finished = finished
self.child = {}
self.cnt = 0
# 트라이 클래스
class Trie:
# 생성시 빈 노드를 생성하여 루트노드로 설정
def __init__(self):
self.root = Node(finished=True)
# 삽입 메소드
def add(self, e):
# 루트 노드에서 탐색 시작
cur = self.root
# 데이터의 각 요소를 키 값으로 하는 노드를 타고내려간다.
for i in e:
# 현재 노드의 자식노드 중에
# 다음 요소를 키 값으로 하는 노드가 존재하지 않는다면 노드를 생성
# 현재 노드의 자식노드 리스트에 삽입한다.
if i not in cur.child:
cur.child[i] = Node(i)
# 해당 노드를 거쳐간 문자열의 수를 1 증가시킨다.
cur.child[i].cnt += 1
cur = cur.child[i]
# 현재 노드가 데이터의 마지막 노드임을 표시
cur.finished = True
# 트라이의 루트노드를 반환
def get_root(self):
return self.root
def sol5670():
# 케이스의 정답 목록을 저장할 리스트
answer = []
for n in sys.stdin:
# 케이스별 영단어의 갯수
n = int(n)
# 단어 리스트
words = [input().strip() for _ in range(n)]
# 트라이에 모든 단어를 삽입
t = Trie()
for word in words:
t.add(word)
# 루트노드의 모든 자식노드들에 대해 dfs 를 실행, 그 결과를 모두 더한다
# res 값은 모든 영단어를 타이핑하기 위해 버튼을 눌러야할 횟수의 총합
res = 0
root = t.get_root()
for cur in root.child.values():
res += dfs(root, cur)
# 평균값을 소숫점 셋째자리에서 반올림하여 answer 리스트에 삽입
answer.append('%.2f' % (res / n))
# 출력형식에 맞춰 정답리스트 반환
return '\n'.join(answer)
# 탐색 함수
def dfs(parent, node):
# 버튼을 눌러야 할 횟수
res = 0
# 현재 노드가 부모노드의 유일한 자식노드이거나
# 부모노드가 데이터의 마지막 노드로 표시되어있을 경우
# 자동완성이 되지 않기 때문에 버튼을 눌러야함
if parent.finished or len(parent.child) > 1:
res += node.cnt
# 자식노드에 대해 탐색함수 재귀호출하여 결과값을 res 에 가산
for c in node.child.values():
res += dfs(node, c)
# 버튼을 눌러야 할 횟수 반환
return res약간의 최적화가 필요하긴 했지만 아슬아슬하게 Python3 으로도 AC를 받을 수 있었다.
'코딩테스트 > 알고리즘' 카테고리의 다른 글
| #34 누적 합(Prefix Sum) - 2차원 (0) | 2021.09.13 |
|---|---|
| #33 누적 합(Prefix Sum) - 1차원 (0) | 2021.09.11 |
| #32 문자열 탐색 - 트라이(Trie) 1 (0) | 2021.09.08 |
| #31 문자열 탐색 - KMP 알고리즘(2) (0) | 2021.09.07 |
| #30 문자열 탐색 - KMP 알고리즘(1) (0) | 2021.09.06 |